Results

The results of a MDDF calculation are returned in a data structure which contains the MDDF, KB integrals, and atomic contributions. The following section will assume that the computation was performed by calling the mddf function with

results = mddf(trajectory, Options(bulk_range=(8.0, 12.0)))

such that the results variable contain the Result data structure. By default, the histograms contain 500 bins (binstep=0.002 and cutoff=10.) such that all data-vectors will contain 500 lines.

To learn how to save and load saved data, read the next section.

The Result data structure: main data

The most important data to be read from results are the distances, minimum-distance distribution function, and KB integrals. These data is stored in the following vectors:

Distances of the histograms: `results.d`

The following vector will contain values ranging from 0. to cutoff, and the distance at each bin is the distance in that bin for which half of the volume of the bin is within d, and half of the volume is above d, if the volume was spherical:

julia> results.d
500-element Array{Float64,1}:
 0.015874010519682
 0.033019272488946275
 ⋮
 9.970010030080179
 9.99001000999998

Minimum-distance distribution function: `results.mddf`

The results.mddf vector will contain the main result, which the minimum-distance distribution function. For a properly-sampled simulation, it will be zero at very short distances and converge to 1.0 for distances smaller than the cutoff:

julia> results.mddf
500-element Array{Float64,1}:
 0.0
 0.0
     ⋮
 0.999052514965403
 1.001030818286187

A typical plot of results.mddf as a function of results.d will look like:

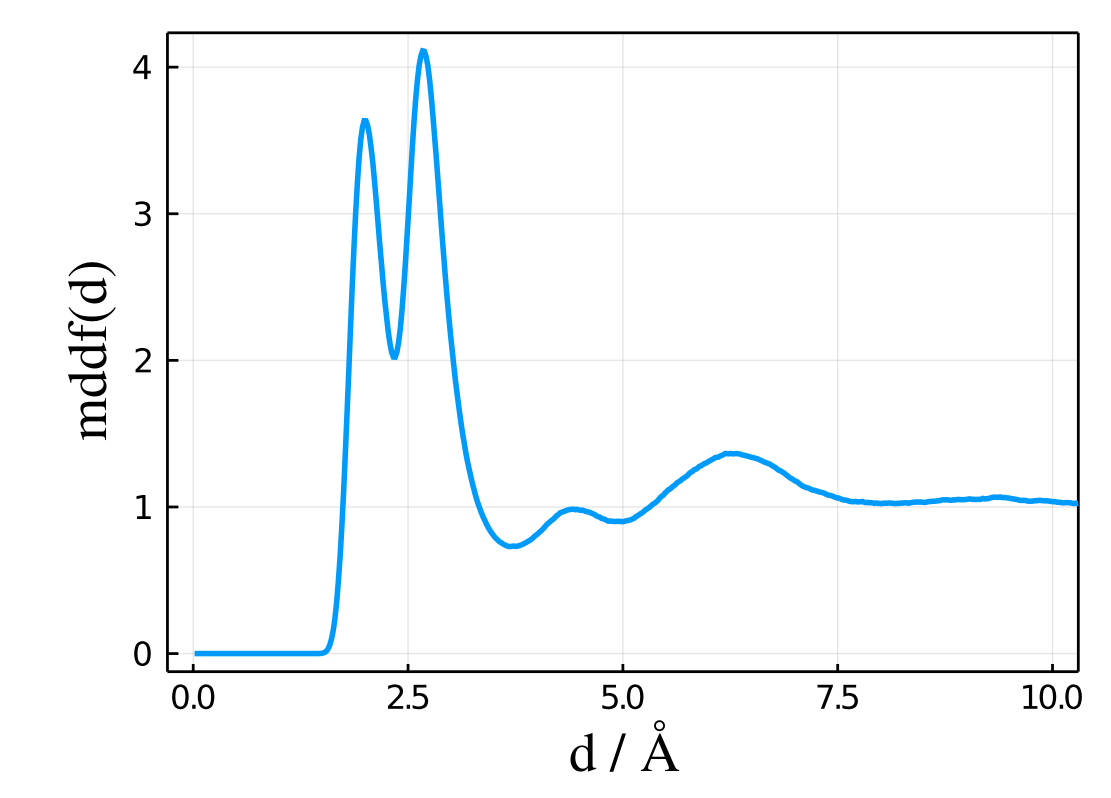
Thus, this plot was obtained with the following code:

using Plots
plot(results.d,results.mddf,xlabel="d/A",ylabel="mddf(d) / L/mol")

Kirkwood-Buff integral: `results.kb`

The results.kb vector will contain the Kirkwood-Buff integral computed as a function of the minimum-distance to the solute. For properly sampled simulations, it is expected to converge at large distances.

julia> results.kb
500-element Array{Float64,1}:
     0.0
    -0.3249356504752985
    -2.9804719721525
     ⋮
    0.72186381783
    1.13624162115

A typical plot of results.kb as a function of results.d will look like:

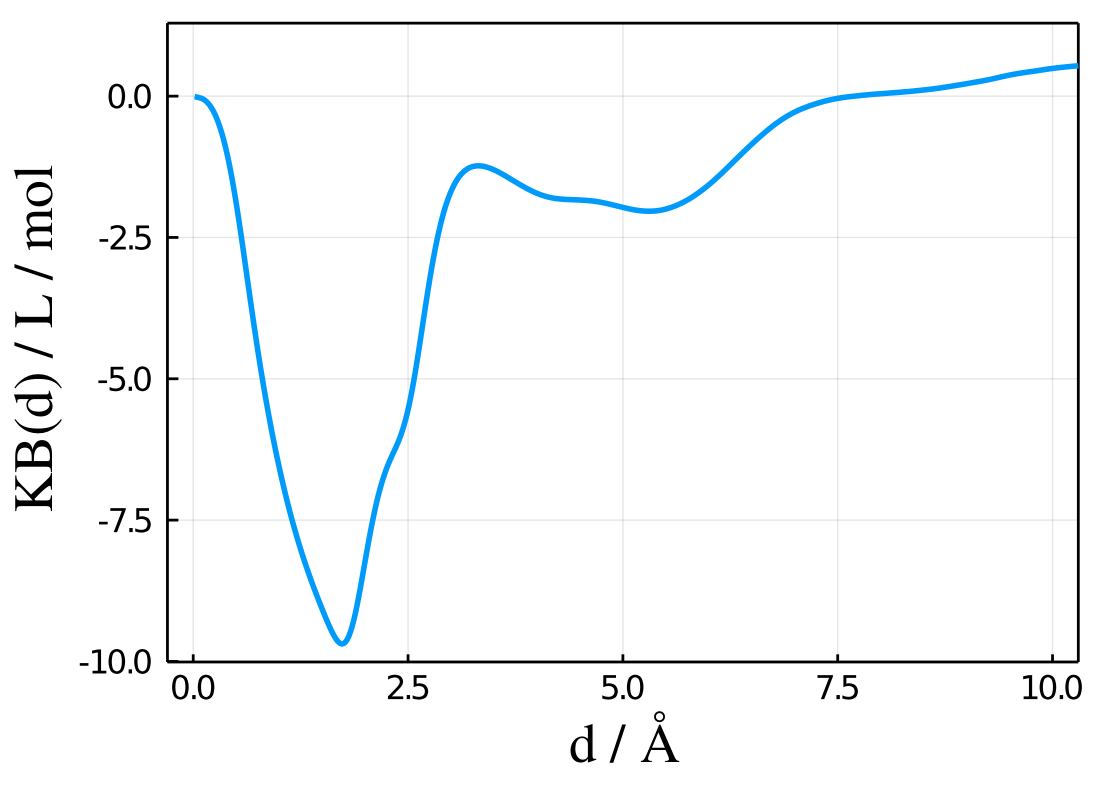
Thus, this plot was obtained with the following code:

using Plots
plot(results.d,results.kb,xlabel="d/A",ylabel="mddf(d) / L/mol")

Units

The distance is assumed to be in Å, as this is the most common distance units in molecular simulations. The coordinates of the atoms are assumed be provided in Å.
The minimum-distance distribution function is unit-less, since it is the ratio of the density at each distance divided by an ideal-gas density.
The Kirkwood-Buff integrals are returned in cm³ mol⁻¹, if the coordinates were provided in Å.

Warning

If the coordinates are not in Å, the calculation will proceed normally, but the units of the KB integrals, which has units of volume per mol, should be converted to conform the length unit provided.

Coordination number and other data

Obtaining the MDDF involves the computation of some intermediate properties that are frequently useful for additional solution structure analysis. In particular, the coordination numbers are computed. For example, the coordination number as a function from the distance to the solute can be retrieved from a Results data structure with:

coordination_number = results.coordination_number

and this data can be plotted against the distances by:

plot(result.d,results.coordination_number)

The coordination number of subgroups can also be obtained, as explained in the Coordination number section.

The complete data available is:

Parameter	Meaning	Type of value	Comment
`d`	Vector of distances of the histograms.	`Vector{Float64}`	To be used as the `x` coordinate on plotting any of the data.
`md_count`	Non-normalized count of minimum distances at each `d`.	`Vector{Float64}`	This is the number of minimum distances found at each histogram bin, without normalization. Usually this is not interesting to analyze, because it is dependent on the bin size.
`md_count_random`	Number of minimum distances found at each histogram bin for the random distribution.	`Vector{Float64}`	This is the normalization required to convert the `md_count` array into the minimum-distance distribution.
`coordination_number`	Cumulative number of sites found for each histogram distance.	`Vector{Float64}`	This is the coordination number, that is, the number of sites found cumulative up to each distance, without any normalization.
`coordination_number_random`	Cumulative site count for the random distribution.	`Vector{Float64}`	Usually not interesting for analysis.
`mddf`	The final distribution function.	`Vector{Float64}`	This is the MDDF computed (`md_count` normalized by `md_count_random`). It is the main result of the calculation.
`kb`	The final Kirkwood-Buff integral.	`Vector{Float64}`	This is the final KB integral, as a function of the integration distance from the solute. Computed as `coordination_number - coordination_number_random`
`solute_atom`	Atomic contributions of the solute.	`Matrix{Float64}`	This is a matrix with `nbins` lines and `solute.natomspermol` columns, containing the atomic contributions of each solute atom to the complete MDDF.
`solvent_atom`	Atomic contributions of the solvent.	`Matrix{Float64}`	This is a matrix with `nbins` lines and `solvent.natomspermol` columns, containing the atomic contributions of each solvent atom to the complete MDDF.
`density.solute`	Density (concentration) of the solute in the complete simulation box.	`Float64`	In units of molecules/$\textrm{\AA}^3$
`density.solvent`	Density (concentration) of the solvent in the complete simulation box.	`Float64`	In units of molecules/$\textrm{\AA}^3$
`density.solvent_bulk`	Density (concentration) of the solute in the bulk region.	`Float64`	In units of molecules/$\textrm{\AA}^3$
`volume`	Volume measures.	`Volume`	Contains the total volume of the simulation, the bulk volume, the volume of the solute domain and the shell volume of each `bin` of the histogram. These are computed by numerical integration from the random distributions.
`files`	List of files read.	`Vector{String}`
`weights`	Weights of each file in the final counts.	`Vector{Float64}`	If the trajectories have different lengths or number of frames, the weights are adapted accordingly.

Other Result parameters available which are set at Options:

Parameter	Meaning	Type of value	Comment
`nbins`	Number of bins of the histograms.	`Int`
`dbulk`	Distance from solute of bulk solution.	`Float64`
`cutoff`	Maximum distance to be considered for histograms.	`Float64`
`autocorrelation`	The solute is the same as the solvent?	`Bool`	Automatically set if `solute == solvent`.
`solute`	Properties of the solute	`AtomSelection`	Contains the number of atoms, number of atoms per molecule and number of molecules of the solute.
`solvent`	Properties of the solvent.	`AtomSelection`	Contains the number of atoms, number of atoms per molecule and number of molecules of the solvent.
`irefatom`	This is a reference atom that is used to generate random rotations and translations internally.	`Int`	Counts of the distributions for this atom are performed automatically to obtain radial (or proximal) distribution functions. Can be used for testing purposes.
`rdf_count`	This is the `md_count` minimum distance count of `irefatom`.	`Vector{Float64}`	This corresponds to the conventional radial distribution function if the solute contains only one atom.
`rdf_count_random`	Minimum distance of `irefatom` count for the random distribution.	`Vector{Float64}`
`rdf`	Distribution function computed from the `irefatom` distribution. It is a conventional `rdf` if the solvent has only one atom.	`Vector{Float64}`
`kb_rdf`	Kirkwood-Buff integral computed from the `irefatom` distribution.	`Vector{Float64}`	This must converge, at long distances, to the same value as `kb`, and can be used for testing.
`options`	Calculation options.	`Options`	Carries (some redundant) options set by the user.
`lastframe_read`	Last frame read from the trajectory.	`Int`
`n_frames_read`	Number of frames read from the trajectory.	`Int`	Can differ from `lastframe_read` if `stride != 1`

Reference functions

ComplexMixtures.Density — Type

mutable struct Density

Structure to contain the density values obtained from the calculation.

solute::Float64
solvent::Float64
solvent_bulk::Float64

source

ComplexMixtures.Result — Type

mutable struct Result

Structure to contain the results of the MDDF calculation.

Version::VersionNumber
nbins::Int64
dbulk::Float64
cutoff::Float64
d::Vector{Float64}
md_count::Vector{Float64}
md_count_random::Vector{Float64}
coordination_number::Vector{Float64}
coordination_number_random::Vector{Float64}
mddf::Vector{Float64}
kb::Vector{Float64}
autocorrelation::Bool
solute::AtomSelection
solvent::AtomSelection
solute_group_count::Vector{Vector{Float64}}
solvent_group_count::Vector{Vector{Float64}}
rdf_count::Vector{Float64}
rdf_count_random::Vector{Float64}
sum_rdf_count::Vector{Float64}
sum_rdf_count_random::Vector{Float64}
rdf::Vector{Float64}
kb_rdf::Vector{Float64}
density::ComplexMixtures.Density
volume::ComplexMixtures.Volume
files::Vector{ComplexMixtures.TrajectoryFileOptions}
weights::Vector{Float64}

The Result{Vector{Float64}} parametric type is necessary only for reading the JSON3 saved file.

source

Base.merge — Method

merge(r::Vector{Result})

This function merges the results of MDDF calculations obtained by running the same analysis on multiple trajectories, or multiple parts of the same trajectory. It returns a Result structure of the same type, with all the functions and counters representing averages of the set provided weighted by the number of frames read in each Result set.

source

ComplexMixtures.load — Method

load(filename::String)

Function to load the json saved results file into the Result data structure.

source

ComplexMixtures.overview — Method

overview(R::Result)

Function that outputs the volumes and densities in the most natural units.

source

ComplexMixtures.save — Method

save(R::Result, filename::String)

Function to write the result data structure to a json file.

source